FUN WITH NUMBERS

Posted on January 29, 2004 by Dave Pollard
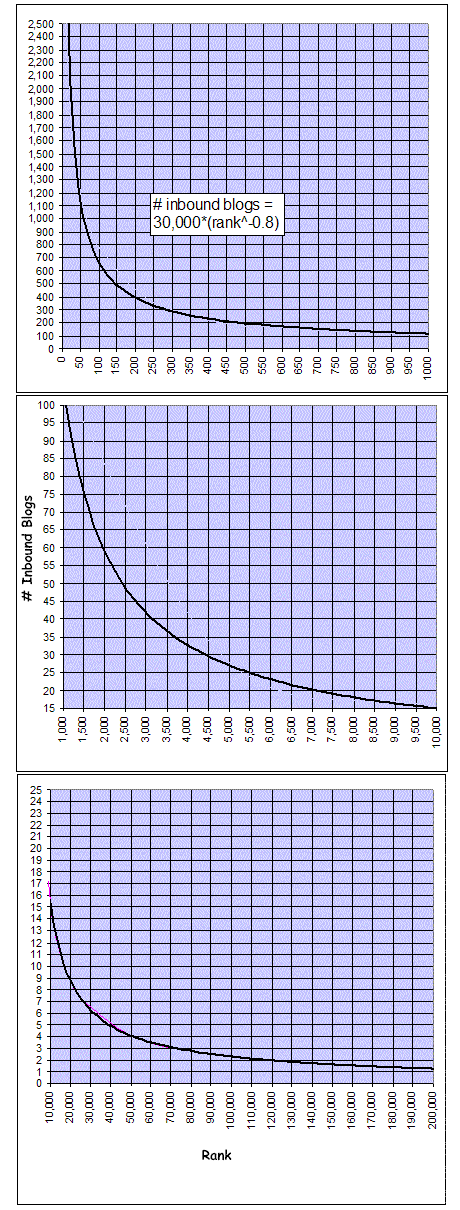
curves
Some fun with blog numbers today. The chart above is as close an approximation as I can derive for Shirky’s Power Curve for the entire blogosphere. I developed it as follows:

  1. I used the number of inbound blogs of Technorati’s Top 100 (from the latest Beta compilation).
  2. I extrapolated this to the Top 500 by overlaying the data for the number of inbound blogs for the blogs ranked #101 to #500 on BlogStreet, another tool that ranks blogs based on number of inbound blogs. BlogStreet tracks a smaller number of blogs (about 150,000) than Technorati (which tracks about 1.5 million), and the number of inbound blogs on their report is generally between 35% (for the most popular blogs) and 85% of the number reported for the same blogs on Technorati.
  3. I then extrapolated the extremely long tail using the best fit power equation for the Top 500. These extrapolations produced an expected value for the #150,000 ranked blog of 9 inbound blogs, and for the #1,000,000 ranked blog of 3 inbound blogs. Since there are many blogs that have zero inbound blogs, this result was clearly implausible
  4. So I went back and cut off the Top 10, and then the Top 50 blogs, and refit the Power Curve for the remainder. This produced a much more logical projection that about 200,000 blogs have one or more inbound blogs, and the top 17,000 blogs have ten or more inbound blogs. This seems plausible to me, but if any one has any contrary data I’d be pleased to incorporate it and refit the curves accordingly.
  5. The formula for this closest fit of the Power Curve is as follows: Forecast number of inbound blogs = 30,000 / (rank 0.8).
  6. The fact that this formula does not apply to the Top 50 is, I think, interesting. The formula would forecast that the #1 blog would have 30,000 inbound blogs (none has anywhere near that) and the #20 ranked blog would have 2700 inbound blogs (per Technorati that blog has only 1900). From #50 on, the formula produces forecasts amazingly close to the actuals. The fact that the curve is (despite all appearances) slightenly flattened at the top end might indicate that there’s a practical limit to how much of an audience any blogger can satisfy, given all the choice out there.
  7. Even if you have no hope of ever making the Top 100, you can use the charts above to estimate your popularity rank in the blogosphere. If you have a mere 5 inbound blogs, you’re probably in the top 40,000 blogs. Ten puts you in the top 17,000, twenty puts you in the top 7,000 (the top 0.5%), fifty puts you in the top 2,400, one hundred almost gets you into the top 1,000, and two hundred almost gets you into the top 400. If you have more inbound blogs than that, you can use BlogStreet to check out your ranking, and if you have eight hundred you know you’re already in the A-list Top 100.

There are of course other measures of popularity besides the number of people that blogroll you. You can track the number of people that subscribe to your RSS feed using Dave Winer’s Share Your OPML site. The Top 10 all have at least 220 subscribers, and the Top 100 all have at least 72. Expect these cutoff numbers to rise quickly as more people register. As for the mug’s game of rating blog by hitcounts, good luck trying to figure out what they mean. From what I’ve seen as many of 90% of the eyeballs that hit your site (notably most of those from Google and other search engines) actually don’t stay around long enough to read anything. If you believe SiteMeter, A-listers get between 1,500 (Alas a Blog), through 6,000 (TBogg) to 15,000 (Eschaton) to 200,000 (Kos) hits per day. Some spikes as high as two million hits per day have been achieved by A-listers for brief periods. At Salon Blogs, average hits per day are about 7 times the number of inbound blogs, so if this ratio applies to the whole blogosphere, a Top 100 A-lister should be getting about 6,000 hits per day, a Top 1000 B-lister should be getting 750 hits per day, and a Top 10,000 C-lister should be getting 100-150 hits per day.

And for those that like big numbers, the aggregate number of inbound blogs for the entire blogosphere works out to about 1.3 million, if the curve above is correct. That would equate to about 10 million hits per day. SiteMeter suggests the average hit keeps eyeballs for 1.5 minutes, which equates to, say, 750,000 blog readers per day spending an average of 20 minutes reading blogs. That’s less than the paid circulation of some big newspapers, and less than 1% of the aggregate time Americans alone spend watching TV news each day. Kinda makes you humble.

This entry was posted in Using Weblogs and Technology. Bookmark the permalink.

6 Responses to FUN WITH NUMBERS

  2. Dave Pollard says:
    January 29, 2004 at 15:55

    Someone e-mailed to say that the above formula is useless because it has the desired independent and dependent variables reversed. So for those who’ve forgotten your high school math that would make the formula: Estimated rank = (30,000/number of inbound blogs)^1.25

  3. Stu Savory says:
    January 29, 2004 at 23:50

    Taking your formula as the linearised-transform-approximation to the data (sorry, but I don’t know the correct English expression), what is the correlation coefficient Dave?PS: I’ve asked you to give R or R^2 on previous occasions too, pls don’t forget, to maintain good science.Stu Savory

  4. Dave Pollard says:
    January 30, 2004 at 08:50

    Stu: Now you’ve trumped my high school math knowledge. I thought r-squared correlation coefficients could only be calculated for linear and polynomial equations, not logarithmic and power equations. When I try to compute it, it shows a second trendline (much worse than the power curve fit), and that second trendline shows an r-squared of .9918. That sounds pretty good, but as I said, the curve flattens noticeably at the top (left) end, and the formula is not accurate for the Top 50 blogs (excluding the Top 50, the r-squared for the formula is .9996). But thanks for keeping me honest, and if you can find some more data that can make this exercise more ‘scientific’, I’d love to play some more ;-)

  5. Stu Savory says:
    January 30, 2004 at 09:46

    Within the range to be interpolated (boundaries should be stated, as you did) you have a formula : Forecast number of inbound blogs = 30,000 / (rank ^0.8), or of course its inverse for the other direction. The R values will be different. By using this transform, you are predicting a variable Y-transformed which is alledgedly linear regressing with X. Since this is linear, you may calculate R and R^2. These are the numbers I’d like to know, in both directions. Then, given your sample size (which you should state) we know the number of degrees of Freedom and can calculate whether or not your results are significant at the 95% and 99% and 99.9% levels. I was just hoping you would do this work for us, after all, it’s no good claiming a result if you don#t know whether it is true!That would just like Dubya, and you don’t want that do you? ;-)Stu

  6. Stu Savory says:
    January 30, 2004 at 20:19

    Dave, I’m not knocking you, I’m just trying to ensure people do not draw wrong conclusions. Please consider this :-The median blog has 8 inbound blogs. Your formula predicts rank 29345. But inbound-blog count is a step function, not a continuous variable. So for an individual the next steps (or noise) might make it 7 or 9 rather than 8 (we’re talking digitalisation errors here).The corresponding predicted ranks for 7 and 9 are 34676 and 25328, a difference of 9348 or a whopping 32% of the predicted median rank. Now ask yourself about the usefulness of the predictor.

Comments are closed.